SVM用于分类任务

自实现核SVM用于分类任务

支持向量机是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。

在这里，考虑基于核方法的支持向量机，并使用SMO算法去训练它，这是LIBSVM和sklearn中训练核SVM的方法，但在project1中我自行实现SMO算法求解器。

SMO算法

SMO（Sequential Minimal Optimization）是求解SVM问题的高效算法之一，libSVM采用的正是该算法。SMO算法其实是一种启发式算法：先选择两个变量 $α_i$ 和 $α_j$ ，然后固定其他参数，从而将问题转化成一个二变量的二次规划问题。求出能使目标最大的一对 $α_i$ 和$α_j$ 后，将它们固定，再选择两个变量，直到目标值收敛。

采用Chang, Chih-Chung, and Chih-Jen Lin. “LIBSVM: a library for support vector machines.” ACM transactions on intelligent systems and technology (TIST) 2.3 (2011): 1-27.中的实现方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
import numpy as np
from functools import lru_cache


class Solver:
    r'''SMO算法求解器，迭代求解下面的问题:
    .. math:: \min_{\pmb\alpha}\quad&\frac12\pmb\alpha^T\pmb Q\pmb\alpha+\pmb p^T\pmb\alpha\\
        \text{s.t.}\quad&\pmb y^T\pmb\alpha=0\\
        &0\leq\alpha_i\leq C,i=1,\cdots,l
    
    Parameters
    ----------
    Q : numpy.ndarray
        优化问题中的 :math:`\pmb Q` 矩阵；
    p : numpy.ndarray
        优化问题中的 :math:`\pmb p` 向量；
    y : numpy.ndarray
        优化问题中的 :math:`\pmb y` 向量；
    C : float
        优化问题中的 :math:`C` 变量；
    tol : float, default=1e-5
        变量选择的tolerance，默认为1e-5.
    '''
    def __init__(self,
                 Q: np.ndarray,
                 p: np.ndarray,
                 y: np.ndarray,
                 C: float,
                 tol: float = 1e-5) -> None:
        problem_size = p.shape[0]
        assert problem_size == y.shape[0]
        if Q is not None:
            assert problem_size == Q.shape[0]
            assert problem_size == Q.shape[1]

        self.Q = Q
        self.p = p
        self.y = y
        self.C = C
        self.tol = tol
        self.alpha = np.zeros(problem_size)

        # Calculate -y·▽f(α)
        self.neg_y_grad = -y * p

    def working_set_select(self):
        r'''工作集选择，这里采用一阶选择:
        .. math:: \pmb{I}_{up}(\pmb\alpha)&=\{t|\alpha_t<C,y_t=1\text{ or }\alpha_t>0,y_t=-1\}\\
                 \pmb{I}_{low}(\pmb\alpha)&=\{t|\alpha_t<C,y_t=-1\text{ or }\alpha_t>0,y_t=1\}\\
                 i&\in\arg\max_{t}\{-y_t\nabla_tf(\pmb\alpha)|t\in\pmb{I}_{up}(\pmb\alpha)\}\\
                 j&\in\arg\max_{t}\{-y_t\nabla_tf(\pmb\alpha)|t\in\pmb{I}_{low}(\pmb\alpha)\}\\
        '''
        Iup = np.argwhere(
            np.logical_or(
                np.logical_and(self.alpha < self.C, self.y > 0),
                np.logical_and(self.alpha > 0, self.y < 0),
            )).flatten()
        Ilow = np.argwhere(
            np.logical_or(
                np.logical_and(self.alpha < self.C, self.y < 0),
                np.logical_and(self.alpha > 0, self.y > 0),
            )).flatten()

        find_fail = False
        try:
            i = Iup[np.argmax(self.neg_y_grad[Iup])]
            j = Ilow[np.argmin(self.neg_y_grad[Ilow])]
        except:
            find_fail = True

        if find_fail or self.neg_y_grad[i] - self.neg_y_grad[j] < self.tol:
            return -1, -1
        return i, j

    def update(self, i: int, j: int, func=None):
        '''变量更新，在保证变量满足约束的条件下对两变量进行更新'''
        Qi, Qj = self.get_Q(i, func), self.get_Q(j, func)
        yi, yj = self.y[i], self.y[j]
        alpha_i, alpha_j = self.alpha[i], self.alpha[j]

        quad_coef = Qi[i] + Qj[j] - 2 * yi * yj * Qi[j]
        if quad_coef <= 0:
            quad_coef = 1e-12

        if yi * yj == -1:
            delta = (self.neg_y_grad[i] * yi +
                     self.neg_y_grad[j] * yj) / quad_coef
            diff = alpha_i - alpha_j
            self.alpha[i] += delta
            self.alpha[j] += delta

            if diff > 0:
                if (self.alpha[j] < 0):
                    self.alpha[j] = 0
                    self.alpha[i] = diff

            else:
                if (self.alpha[i] < 0):
                    self.alpha[i] = 0
                    self.alpha[j] = -diff

            if diff > 0:
                if (self.alpha[i] > self.C):
                    self.alpha[i] = self.C
                    self.alpha[j] = self.C - diff

            else:
                if (self.alpha[j] > self.C):
                    self.alpha[j] = self.C
                    self.alpha[i] = self.C + diff

        else:
            delta = (self.neg_y_grad[j] * yj -
                     self.neg_y_grad[i] * yi) / quad_coef
            sum = self.alpha[i] + self.alpha[j]
            self.alpha[i] -= delta
            self.alpha[j] += delta

            if sum > self.C:
                if self.alpha[i] > self.C:
                    self.alpha[i] = self.C
                    self.alpha[j] = sum - self.C

            else:
                if self.alpha[j] < 0:
                    self.alpha[j] = 0
                    self.alpha[i] = sum

            if sum > self.C:
                if self.alpha[j] > self.C:
                    self.alpha[j] = self.C
                    self.alpha[i] = sum - self.C

            else:
                if self.alpha[i] < 0:
                    self.alpha[i] = 0
                    self.alpha[j] = sum

        delta_i = self.alpha[i] - alpha_i
        delta_j = self.alpha[j] - alpha_j
        self.neg_y_grad -= self.y * (delta_i * Qi + delta_j * Qj)
        return delta_i, delta_j

    def calculate_rho(self) -> float:
        r'''计算偏置项
        
        .. math:: \rho=\dfrac{\sum_{i:0<\alpha_i<C}y_i\nabla_if(\pmb\alpha)}{|\{i\vert0<\alpha_i<C\}|}
        如果不存在满足条件的支持向量，那么
        .. math:: -M(\pmb\alpha)&=\max\{y_i\nabla_if(\pmb\alpha)|\alpha_i=0,y_i=-1\text{ or }\alpha_i=C,y_i=1\}\\
                  -m(\pmb\alpha)&=\max\{y_i\nabla_if(\pmb\alpha)|\alpha_i=0,y_i=1\text{ or }\alpha_i=C,y_i=-1\}\\
                  \rho&=-\dfrac{M(\pmb\alpha)+m(\pmb\alpha)}{2}
        '''
        sv = np.logical_and(
            self.alpha > 0,
            self.alpha < self.C,
        )
        if sv.sum() > 0:
            rho = -np.average(self.neg_y_grad[sv])
        else:
            ub_id = np.logical_or(
                np.logical_and(self.alpha == 0, self.y < 0),
                np.logical_and(self.alpha == self.C, self.y > 0),
            )
            lb_id = np.logical_or(
                np.logical_and(self.alpha == 0, self.y > 0),
                np.logical_and(self.alpha == self.C, self.y < 0),
            )
            rho = -(self.neg_y_grad[lb_id].min() +
                    self.neg_y_grad[ub_id].max()) / 2
        return rho

    def get_Q(self, i: int, func=None):
        '''获取核矩阵的第i行/列，即
        
        .. math:: [K(\pmb x_1, \pmb x_i),\cdots,K(\pmb x_l, \pmb x_i)]
        '''
        return self.Q[i]

SVM接口的实现

为了让模型能够进行参数选择等功能，按照sklearn接口的模式编写SVM模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
from sklearn.base import BaseEstimator
from sklearn.metrics import accuracy_score
from solver import Solver, SolverWithCache


class BiLinearSVC(BaseEstimator):
    r'''二分类线性SVM，该类被多分类LinearSVC继承，所以不需要使用它。
    
    通过求解对偶问题
    .. math:: \min_{\pmb\alpha}\quad&\dfrac12\pmb\alpha^\top Q\pmb\alpha-\pmb{e}^\top\pmb{\alpha}\\
        \text{s.t.}\quad& \pmb{y}^\top\pmb\alpha=0,\\
        &0\leqslant\alpha_i\leqslant C,i=1,\cdots ,l
    得到决策边界
    .. math:: f(\pmb x)=\sum_{i=1}^ly_i\alpha_i\pmb x_i^T\pmb x-\rho
    Parameters
    ----------
    C : float, default=1
        SVM的正则化参数，默认为1；
    max_iter : int, default=1000
        SMO算法迭代次数，默认1000；
    tol : float, default=1e-5
        SMO算法的容忍度参数，默认1e-5；
    cache_size : int, default=256
        lru缓存大小，默认256，如果为0则不使用缓存，计算Q矩阵然后求解.
    '''
    def __init__(self,
                 C: float = 1.,
                 max_iter: int = 1000,
                 tol: float = 1e-5,
                 cache_size: int = 256) -> None:
        super().__init__()
        self.C = C
        self.max_iter = max_iter
        self.tol = tol
        self.cache_size = cache_size

    def fit(self, X: np.ndarray, y: np.ndarray):
        '''训练模型
        Parameters
        ----------
        X : np.ndarray
            训练集特征;
        y : np.array
            训练集标签，建议0为负标签，1为正标签.
        '''
        X, y = np.array(X), np.array(y, dtype=float)
        y[y != 1] = -1
        l, self.n_features = X.shape
        p = -np.ones(l)

        w = np.zeros(self.n_features)
        if self.cache_size == 0:
            Q = y.reshape(-1, 1) * y * np.matmul(X, X.T)
            solver = Solver(Q, p, y, self.C, self.tol)
        else:
            solver = SolverWithCache(p, y, self.C, self.tol, self.cache_size)

        def func(i):
            return y * np.matmul(X, X[i]) * y[i]

        for n_iter in range(self.max_iter):
            i, j = solver.working_set_select()
            if i < 0:
                break

            delta_i, delta_j = solver.update(i, j, func)
            w += delta_i * y[i] * X[i] + delta_j * y[j] * X[j]
        else:
            print("LinearSVC not coverage with {} iterations".format(
                self.max_iter))

        self.coef_ = (w, solver.calculate_rho())
        return self

    def decision_function(self, X: np.ndarray) -> np.ndarray:
        '''决策函数，输出预测值'''
        return np.matmul(self.coef_[0], np.array(X).T) - self.coef_[-1]

    def predict(self, X: np.ndarray) -> np.ndarray:
        '''预测函数，输出预测标签(0-1)'''
        return (self.decision_function(np.array(X)) >= 0).astype(int)

    def score(self, X: np.ndarray, y: np.ndarray) -> float:
        '''评估函数，给定特征和标签，输出正确率'''
        return accuracy_score(y, self.predict(X))

模型训练

选用UCI数据集中的威斯康辛乳腺癌数据作为实验数据集，首先查看数据分布等信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np
from tqdm import tqdm
from sklearn.preprocessing import LabelEncoder


# 读取数据集
def read_wdbc():
    feature_list, target_list = [], []
    with open("data/wdbc.data", "r") as f:
        lines = f.readlines()
    for line in tqdm(lines, desc='reading data'):
        line_split = line.split(',')[1:]
        feature_list.append(line_split[1:])
        target_list.append(line_split[0])
    return (
        np.array(feature_list).astype(float),
        LabelEncoder().fit_transform(np.array(target_list)),
    )


X, y = read_wdbc()
print(X.shape, y.shape)
reading data: 100%|██████████████████████████████████████████████████████████████████████████| 569/569 [00:00<?, ?it/s]

(569, 30) (569,)

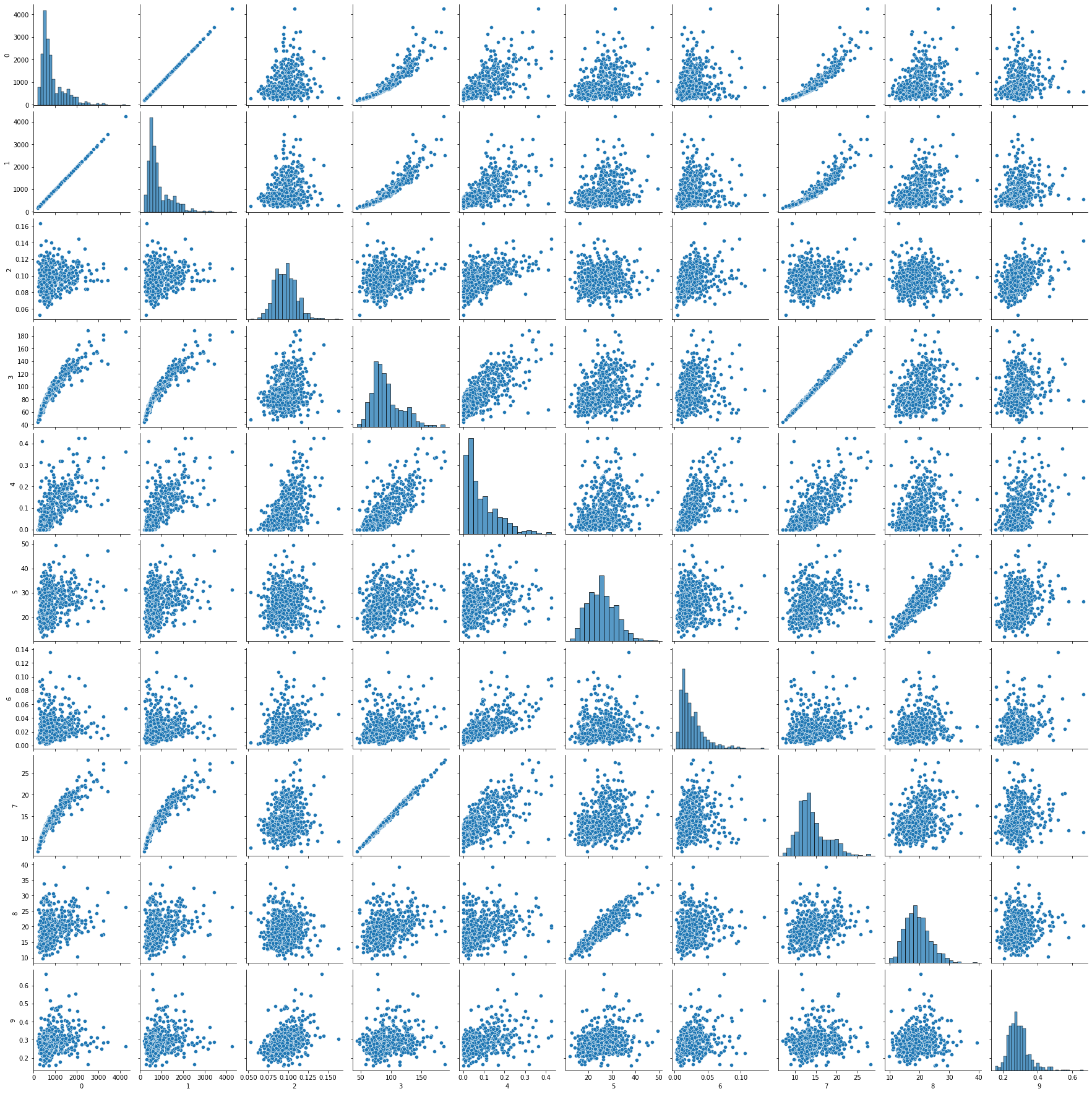
随机选10个特征观察相关性，注意到一些特征间存在很强的线性相关性，此外，很多特征的分布是近似正态分布，比较适合SVM模型分类。

1
2
3
4
5
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd

sns.pairplot(pd.DataFrame(X[:, np.random.randint(0, 30, 10)]))
<seaborn.axisgrid.PairGrid at 0x1a6c91c4d90>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from svm import BiLinearSVC, BiKernelSVC

# 训练集测试集划分
train_X, test_X, train_y, test_y = train_test_split(
    X,
    y,
    train_size=0.8,
    random_state=42,
)

# 数据归一化
stder = MinMaxScaler().fit(train_X)
train_X = stder.transform(train_X)
test_X = stder.transform(test_X)

# 线性核SVM和RBF核SVM
linear_model = BiLinearSVC().fit(train_X, train_y)
rbf_model = BiKernelSVC().fit(train_X, train_y)
acc1 = linear_model.score(test_X, test_y)
acc2 = rbf_model.score(test_X, test_y)
print("LinearSVM : {:2.4f}%, Kernel SVM : {:2.4f}%".format(
    acc1 * 100, acc2 * 100))

LinearSVM : 98.2456%, Kernel SVM : 96.4912%

在Project1中，似乎线性分类器比核RBF效果更好。

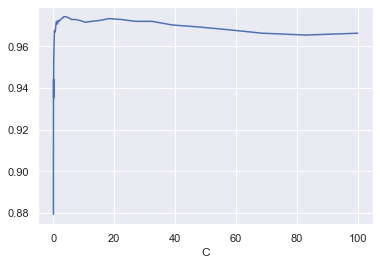
参数选择

线性SVM只有一个超参数$C$，观察不同$C$情况下模型的表现，同时选出最优参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from warnings import filterwarnings

filterwarnings('ignore')
C_list = np.logspace(-2, 2, 50)
n_iter = 20
score_matrix = np.zeros((len(C_list), n_iter))
for i in tqdm(range(n_iter)):
    train_X, test_X, train_y, test_y = train_test_split(
        X,
        y,
        train_size=0.8,
    )
    stder = MinMaxScaler().fit(train_X)
    train_X = stder.transform(train_X)
    test_X = stder.transform(test_X)
    for j, C in enumerate(C_list):
        score_matrix[j, i] = BiLinearSVC(C=C, max_iter=2500).fit(
            train_X,
            train_y,
        ).score(
            test_X,
            test_y,
        )

import seaborn as sns

sns.set()

mean_score = score_matrix.mean(1)
plt.plot(C_list, mean_score, label='Test accuracy')
plt.xlabel("C")
plt.show()
print("best C : {}, best accuracy : {:2.4f}%".format(
    C_list[mean_score.argmax()],
    mean_score.max() * 100,
))
100%|██████████████████████████████████████████████████████████████████████████████████| 20/20 [00:46<00:00,  2.32s/it]

best C : 3.3932217718953264, best accuracy : 97.4123%

接下来看核SVM的表现，首先用不同的核函数进行实验，发现性能最优的是RBF。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
kernel_list = ["rbf", "poly", "sigmoid"]
n_iter = 20

score_matrix = np.zeros((len(kernel_list), n_iter))
for i in tqdm(range(n_iter)):
    train_X, test_X, train_y, test_y = train_test_split(
        X,
        y,
        train_size=0.8,
    )
    stder = MinMaxScaler().fit(train_X)
    train_X = stder.transform(train_X)
    test_X = stder.transform(test_X)
    for j, kernel in enumerate(kernel_list):
        score_matrix[j, i] = BiKernelSVC(
            kernel=kernel,
            max_iter=5000,
        ).fit(
            train_X,
            train_y,
        ).score(
            test_X,
            test_y,
        )

for i, kernel in enumerate(kernel_list):
    print("{:7s}, mean : {:4.2f}%, std : {}".format(
        kernel,
        score_matrix[i].mean() * 100,
        (score_matrix[i] * 100).std(),
    ))

100%|██████████████████████████████████████████████████████████████████████████████████| 20/20 [00:00<00:00, 22.79it/s]

rbf    , mean : 96.80%, std : 1.8664844588555454
poly   , mean : 94.96%, std : 1.9392711376696599
sigmoid, mean : 96.36%, std : 1.2490377952542226

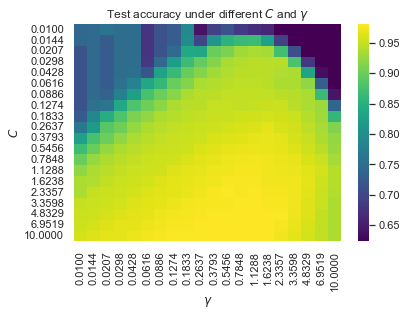
接下来为RBF选取最优参数$C,\gamma$：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
C_list = np.logspace(-2, 1, 20)
G_list = np.logspace(-2, 1, 20)
n_iter = 20
score_matrix = np.zeros((len(C_list), len(G_list), n_iter))
for i in tqdm(range(n_iter)):
    train_X, test_X, train_y, test_y = train_test_split(
        X,
        y,
        train_size=0.8,
    )
    stder = MinMaxScaler().fit(train_X)
    train_X = stder.transform(train_X)
    test_X = stder.transform(test_X)
    for j, C in enumerate(C_list):
        for k, gamma in enumerate(G_list):
            score_matrix[j, k, i] = BiKernelSVC(
                C=C,
                gamma=gamma,
                max_iter=2500,
            ).fit(
                train_X,
                train_y,
            ).score(
                test_X,
                test_y,
            )
100%|██████████████████████████████████████████████████████████████████████████████████| 20/20 [04:21<00:00, 13.06s/it]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
sns.heatmap(
    score_matrix.mean(-1),
    cmap='viridis',
    xticklabels=["{:.4f}".format(x) for x in G_list],
    yticklabels=["{:.4f}".format(x) for x in C_list],
)
plt.xlabel(r"$\gamma$")
plt.ylabel(r"$C$")
plt.title(r"Test accuracy under different $C$ and $\gamma$")
plt.show()
argmax = score_matrix.mean(-1).argmax()
argmax_row, argmax_col = argmax // len(G_list), argmax % len(G_list)
print("Best parameters : C={:.4f}, γ={:.4f}, acc={:.2f}%".format(
    C_list[argmax_row],
    G_list[argmax_col],
    score_matrix.mean(-1).flatten()[argmax] * 100,
))
Best parameters : C=6.9519, γ=1.1288, acc=98.11%
机器学习
#原创
SVM用于分类任务
http://example.com/2023/05/08/SVM用于分类任务/
作者
Zhang Xixiang
发布于
2023年5月8日
许可协议